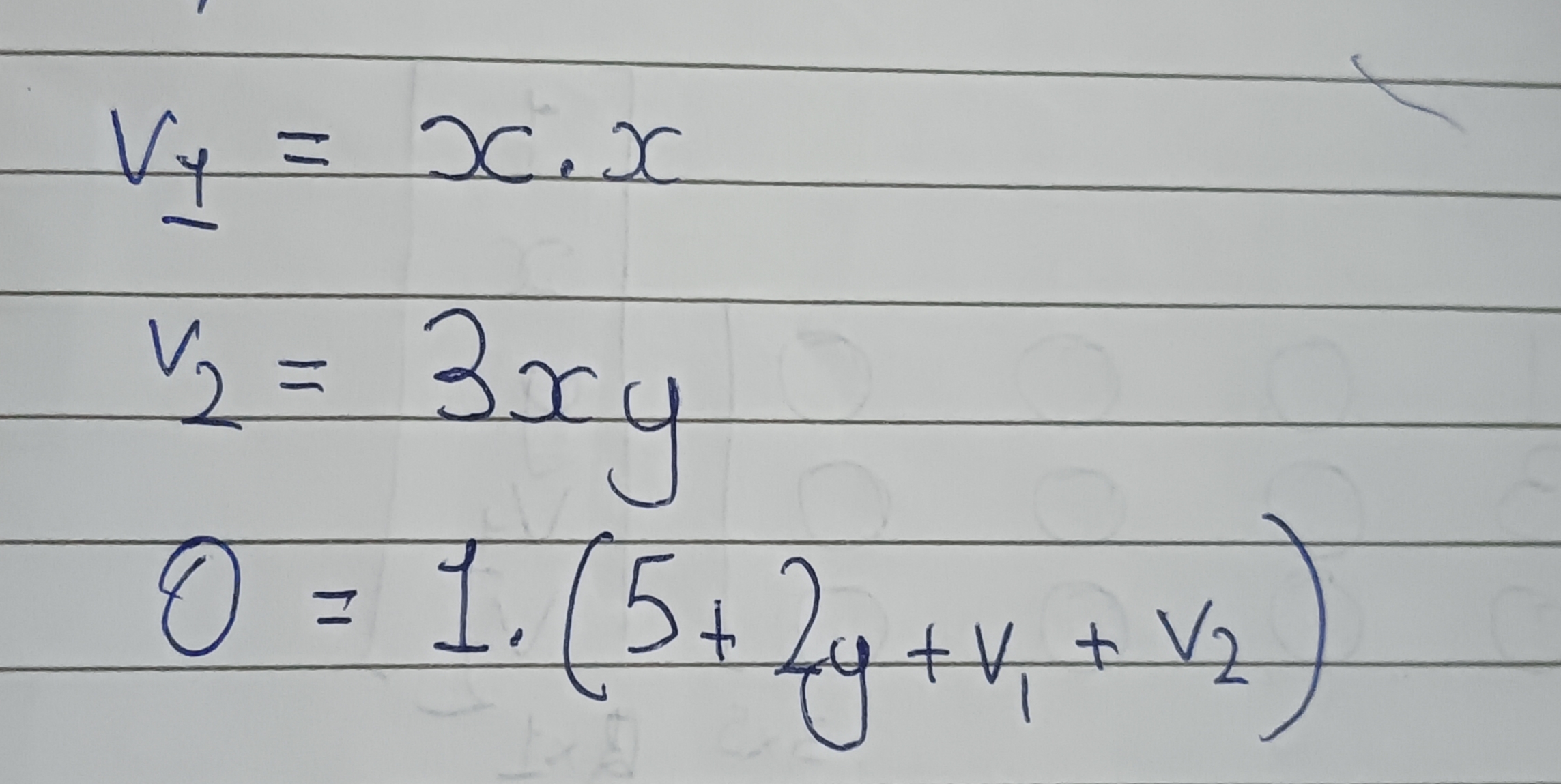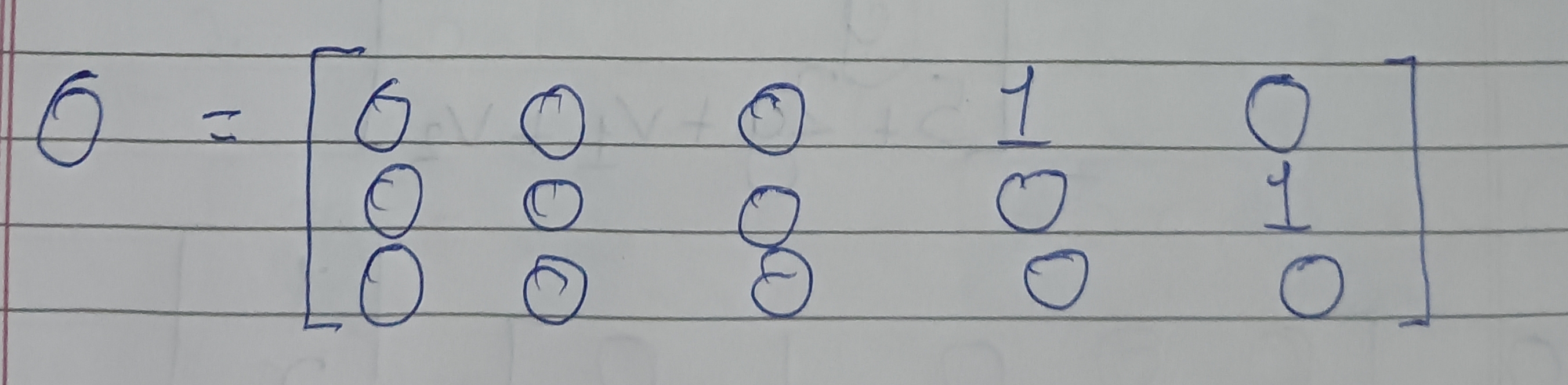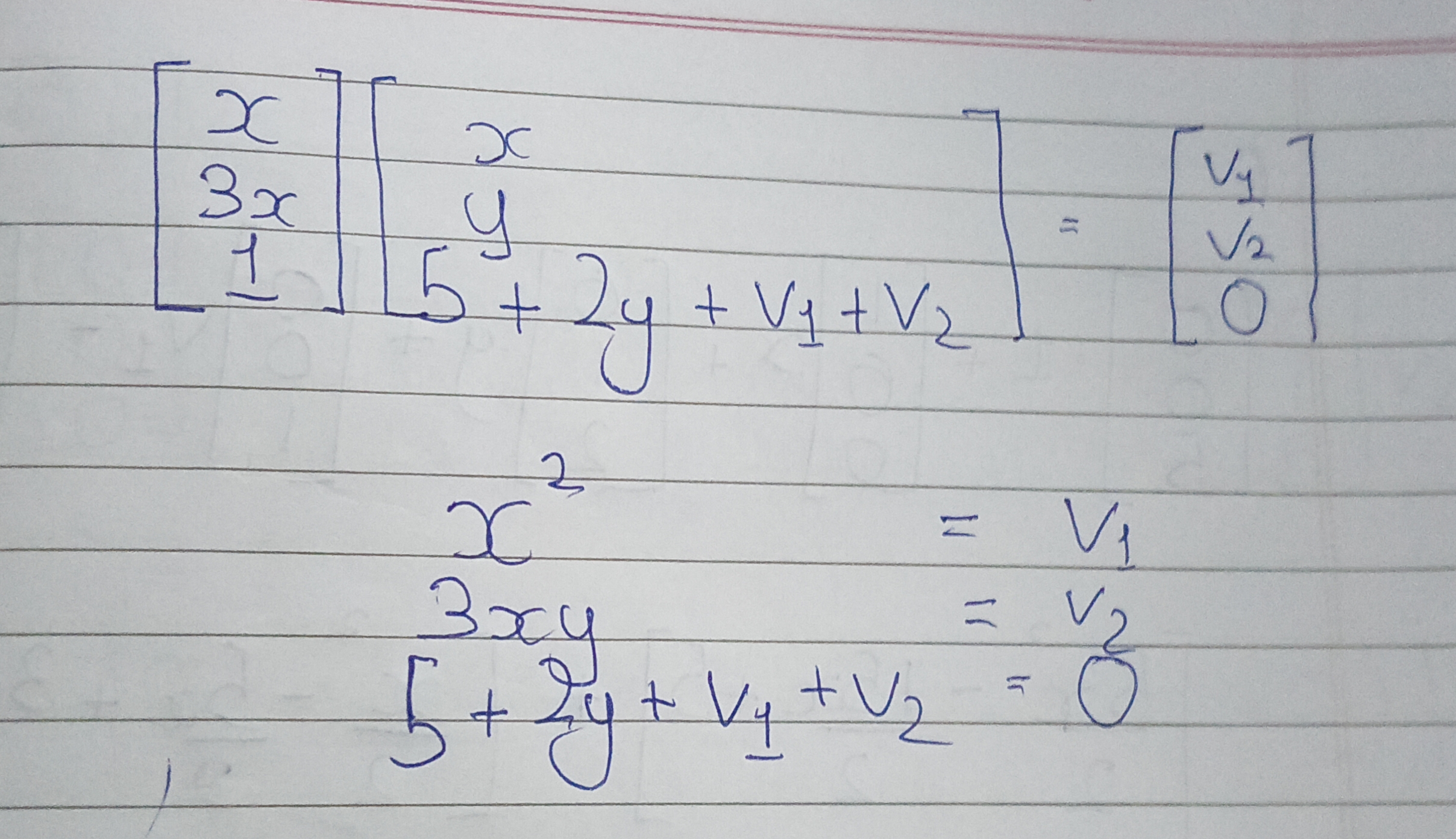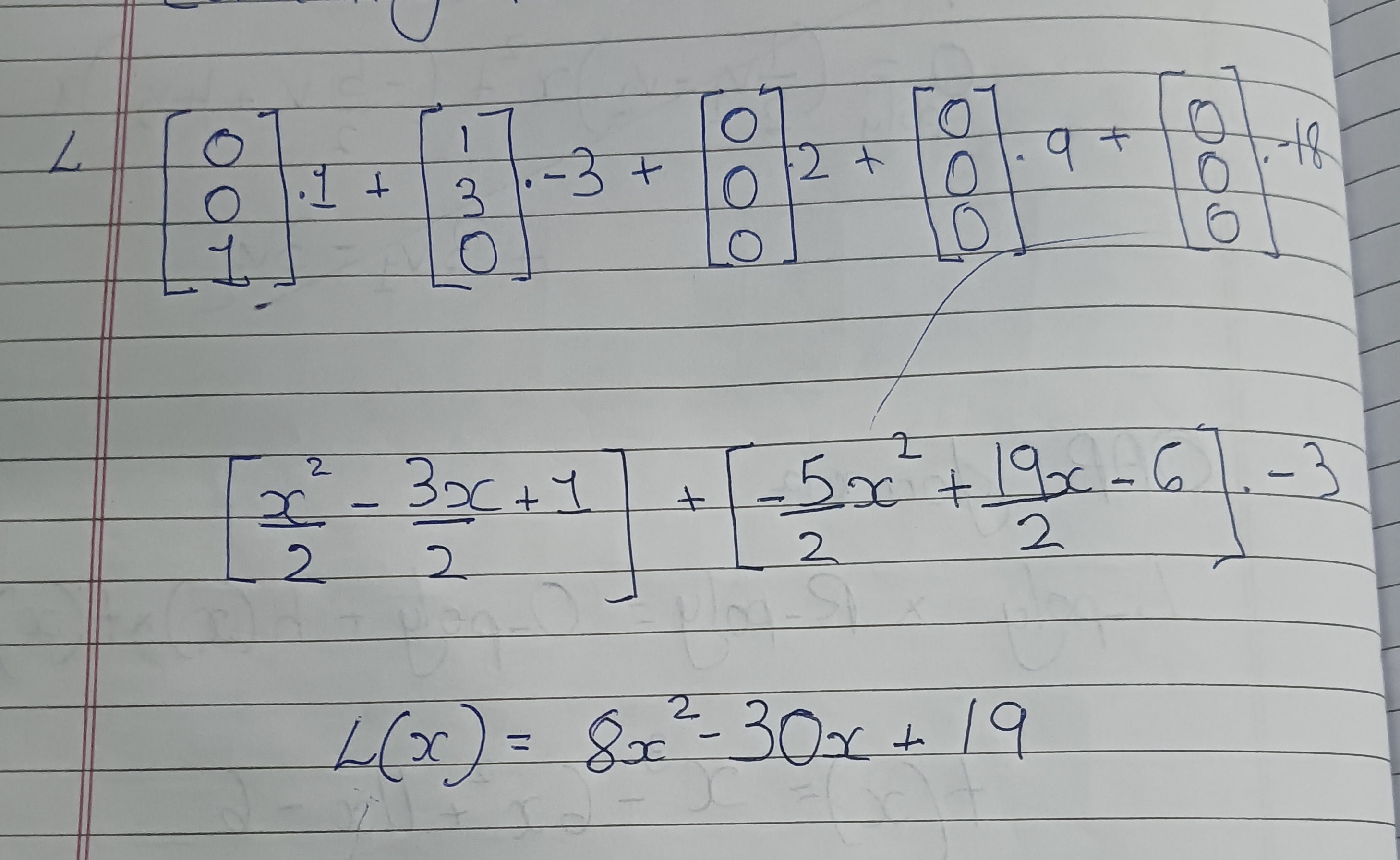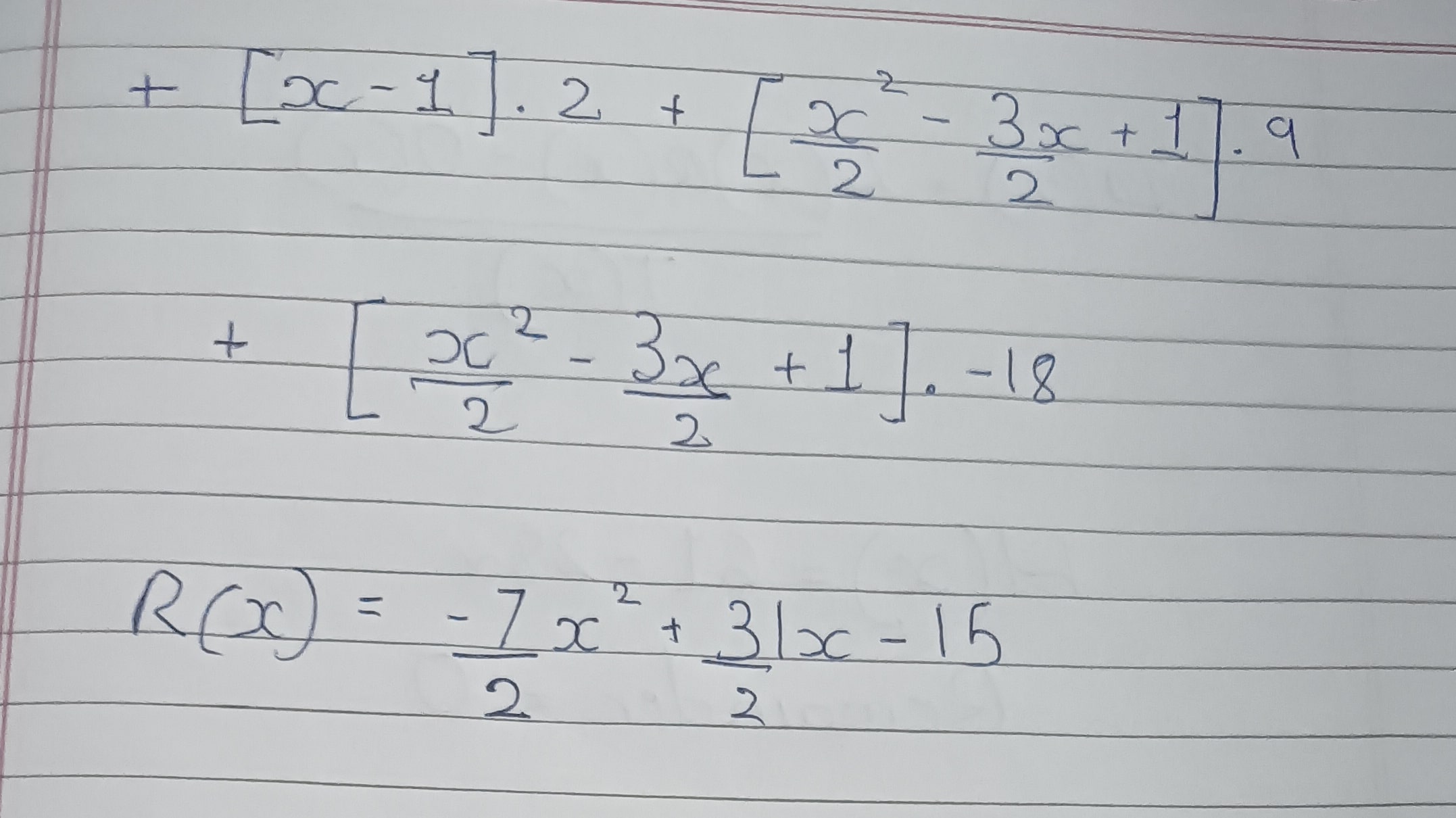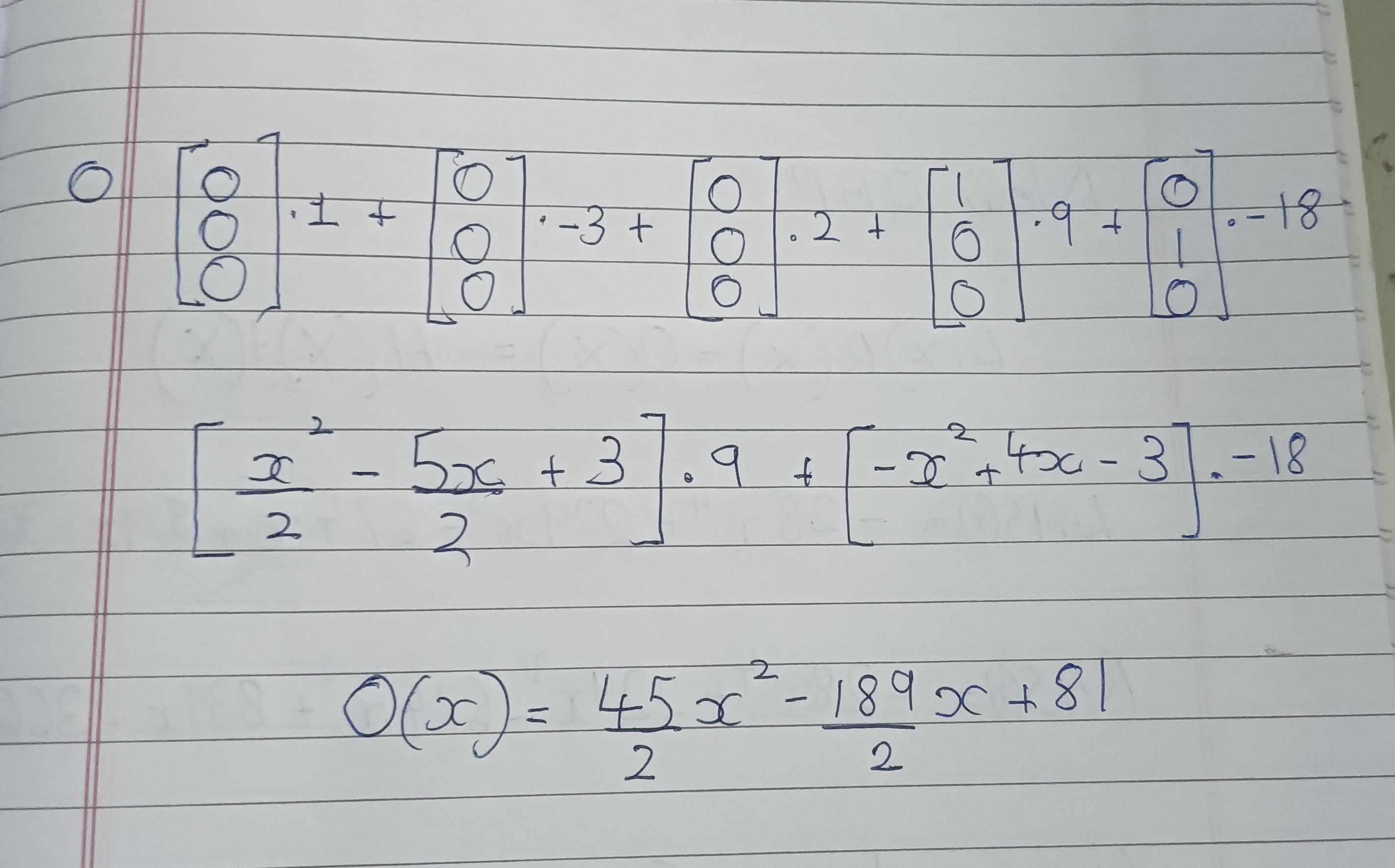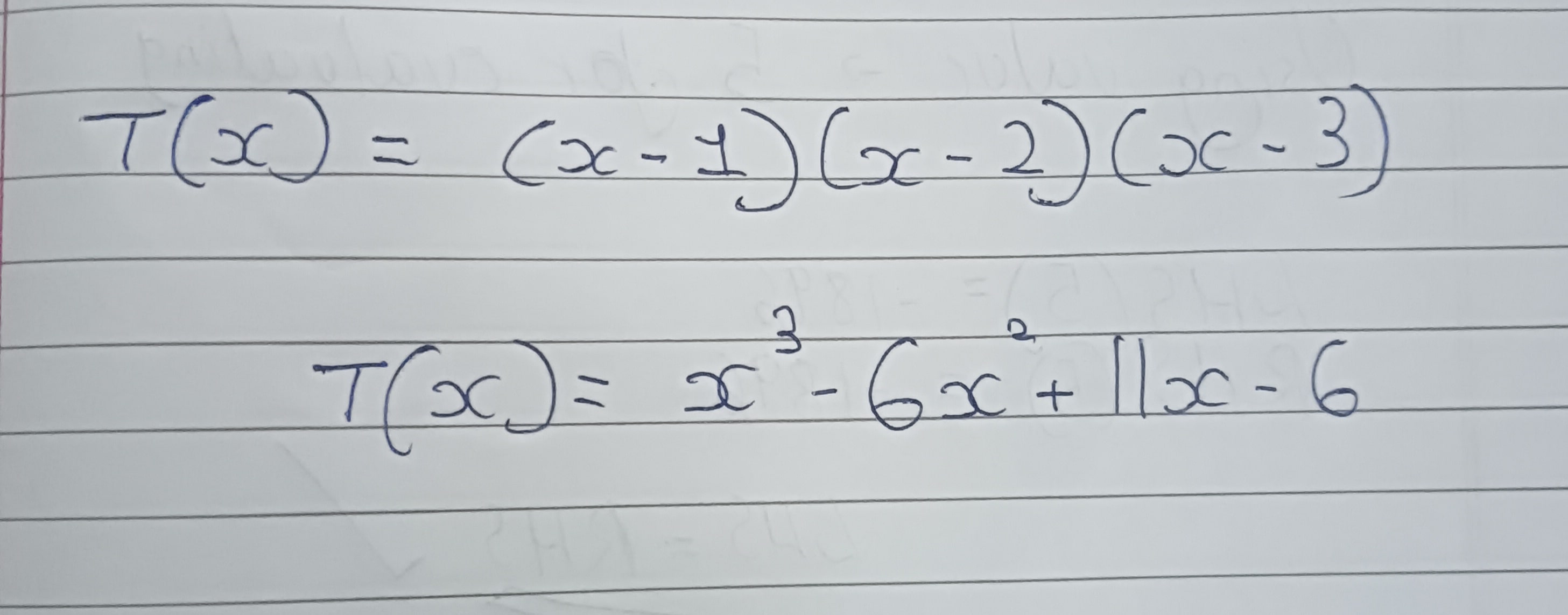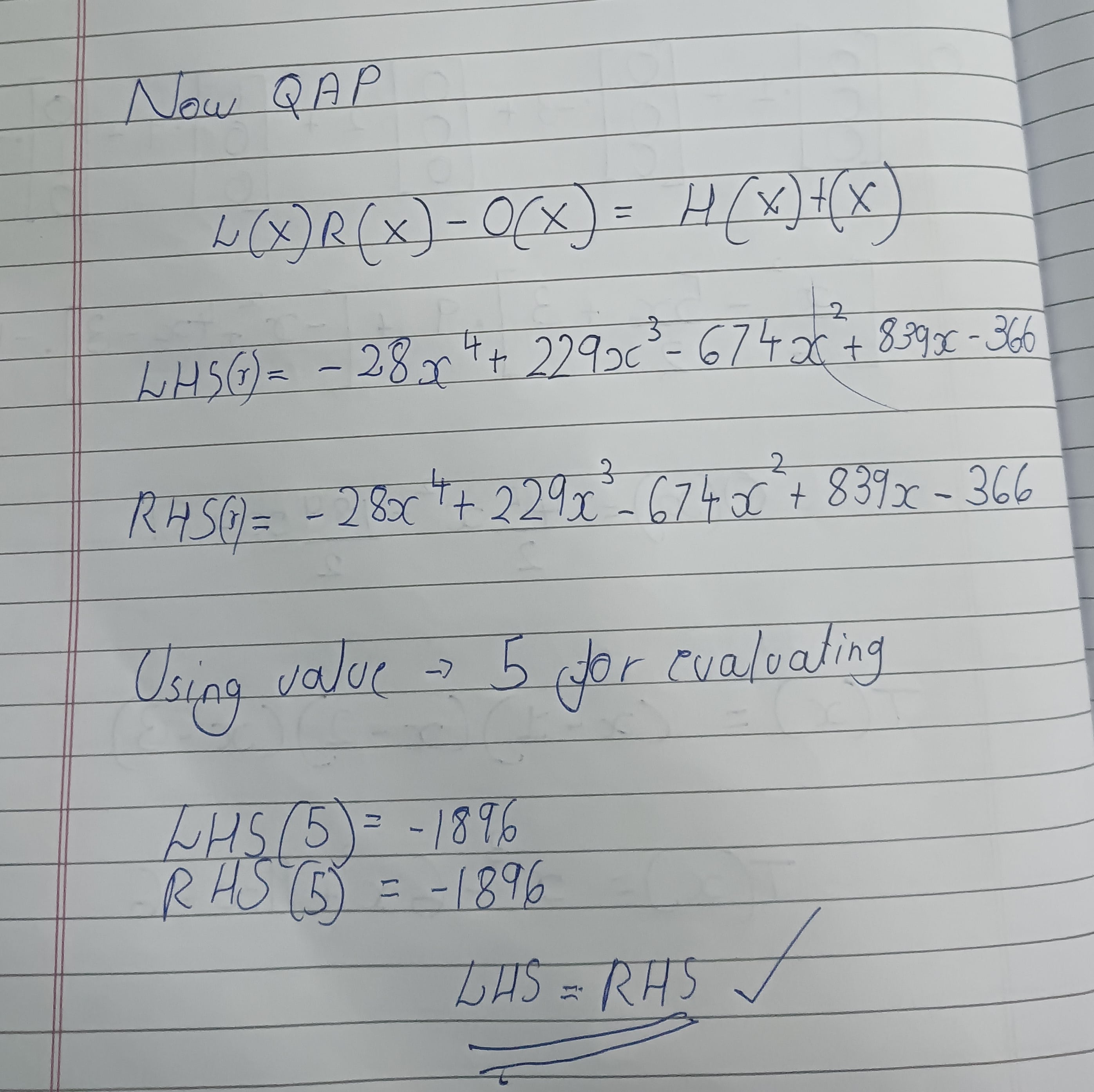Zero Knowledge Proofs - Polynomial to QAP on paper
From a polynomial to R1CS to a QAP without skipping a single step!
So I’ve really been into this for quite some time now; I mean, the rareskills.io book on zk proofs is literally just insane, and honestly, I’m kind of surprised that I’ve made it this far. Yeah, so the primary reason why I’m writing this post is because I didn’t see any complete example of converting an example polynomial to QAP without skipping any single steps anywhere online. I mean, obviously, yeah, that’d be something you’d be doing after learning as an exercise, perhaps? Either way, yeah, here is mine where I take a random polynomial and do the full process on paper.
There’s this chapter from the book https://rareskills.io/post/r1cs-to-qap where they take a polynomial and do the full process, so I’d be doing something like that but completely on paper, drawing every single matrix, including the column ones, and secondly and most importantly, no finite fields. I mean, it isn’t really going to make that much of a difference, but either way, it’d be much easier to visualize for people who aren’t so math friendly.
Again this is a post not explaining these concepts but rather just going down each steps.
Here are the different steps we’ll be doing when converting a polynomial to QAP:
- First, yeah, take a polynomial.
- Convert into its different constraints.
- Get the L, R, and O matrix.
- Checking if it’s correct.
- Taking an example witness vector.
- Convert each column of the L, R, and O vectors to polynomials using Lagrange’s interpolation.
- Multiplying each column with the corresponding elements from the witness vector.
- Getting the H(x) and T(x) polys.
- Using the QAP formula and getting our final result.
- Evaluate the polynomials using a random value.
If we get the LHS and RHS equal, then yeah, we’ve successfully verified it. One more thing is that we can see if we’ve made any mistakes along the way if the remainder when dividing the numerator with t(x) when computing h(x) is zero or non-zero. If we get a zero remainder, we are indeed correct!
1. Choosing a polynomial
So the polynomial I’d be choosing here is this:
\[x^2 + 3xy + 2y + 5 = 0\]2. Converting it into it’s different constraints.
Now our witness vector is going to be of the form: [1, x, y, v1, v2]
We’ll be plugging in values later.
3. Get the L, R, and O matrix.
- This process is really simple since we just have 3 constraints and witness vector consists of 5 elements.
- So 5 columns and 3 rows.
https://rareskills.io/post/rank-1-constraint-system
L matrix:
R matrix:
O matrix:
4. Checking if it’s correct
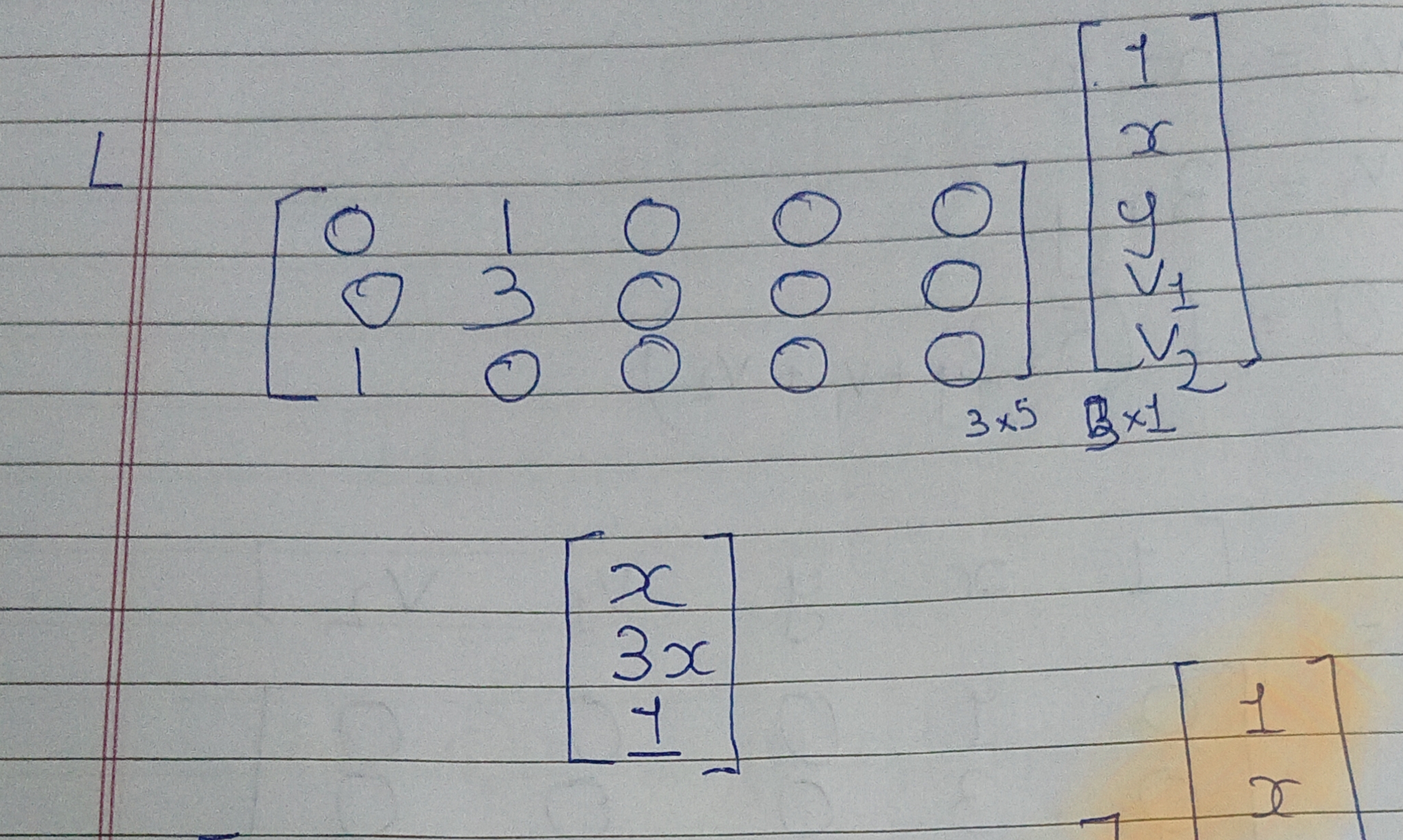
- Now let’s see if the matrix is correct by multiplying with the witness vectors and see if this equality holds:
- La * Ra = Oa
- Where a is our witness vector.
Testing L:
1
2
3
4
5
[
x
3x
1
]
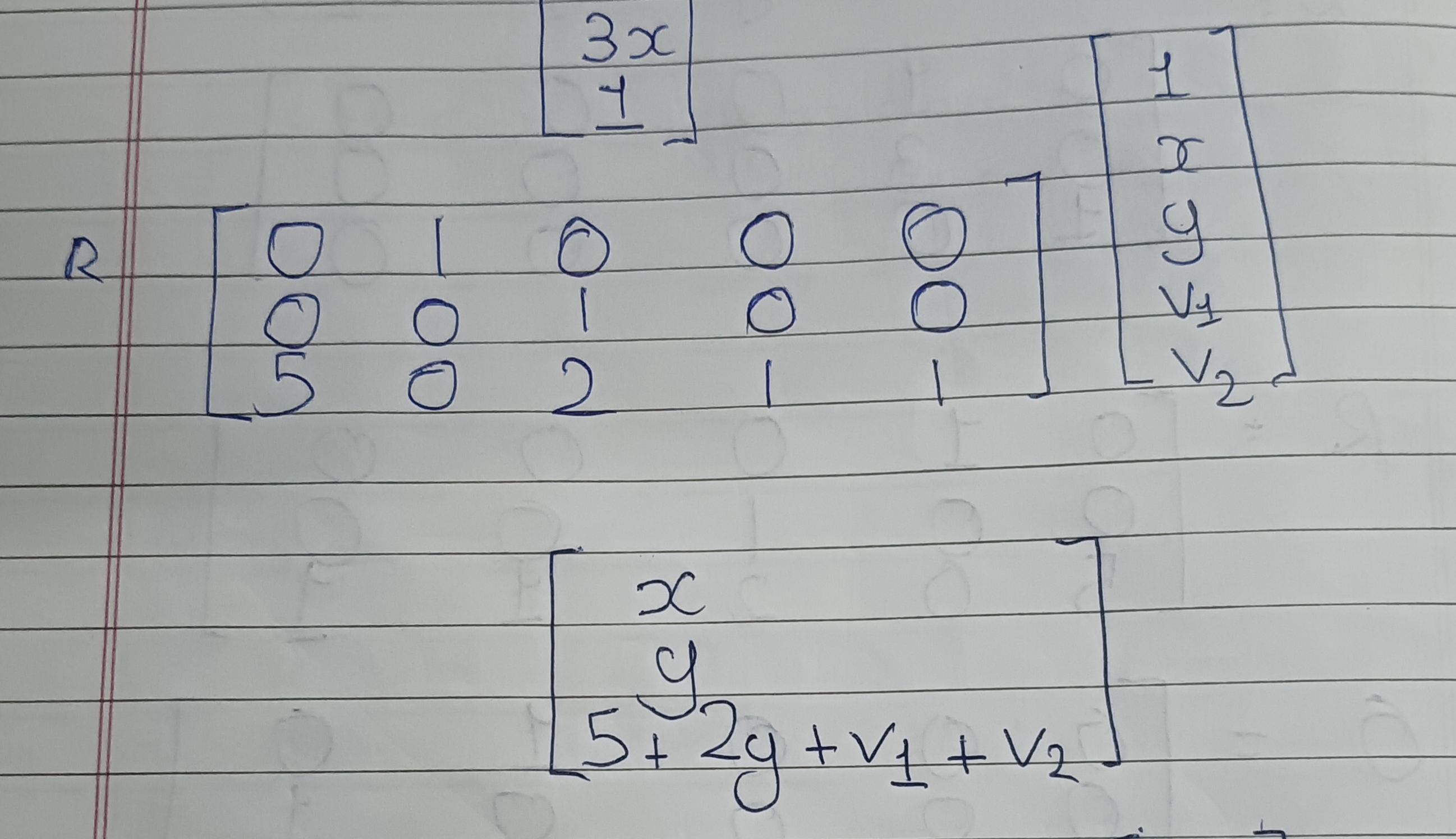
Testing R:
1
2
3
4
5
[
x
y
5 + 2y + v1 + v2
]
Testing O:
1
2
3
4
5
[
v1
v2
0
]
Veryfing LHS and RHS
- As we can see that the matrixs are indeed correct!
5. Taking an example witness vector.
- You can technically plug in an x value and get a y value, I’ll be using this:
1
2
[1, -3, 2, 9, -18]
[1, x, y, v1, v2]
Which is our witness vector.
Now the ongoing to the most important step:
6. Using Lagrange’s interpolation and converting the each column of L, R and O columns to their corresponding polynomials.
Aight so first let’s start with the L matrix:
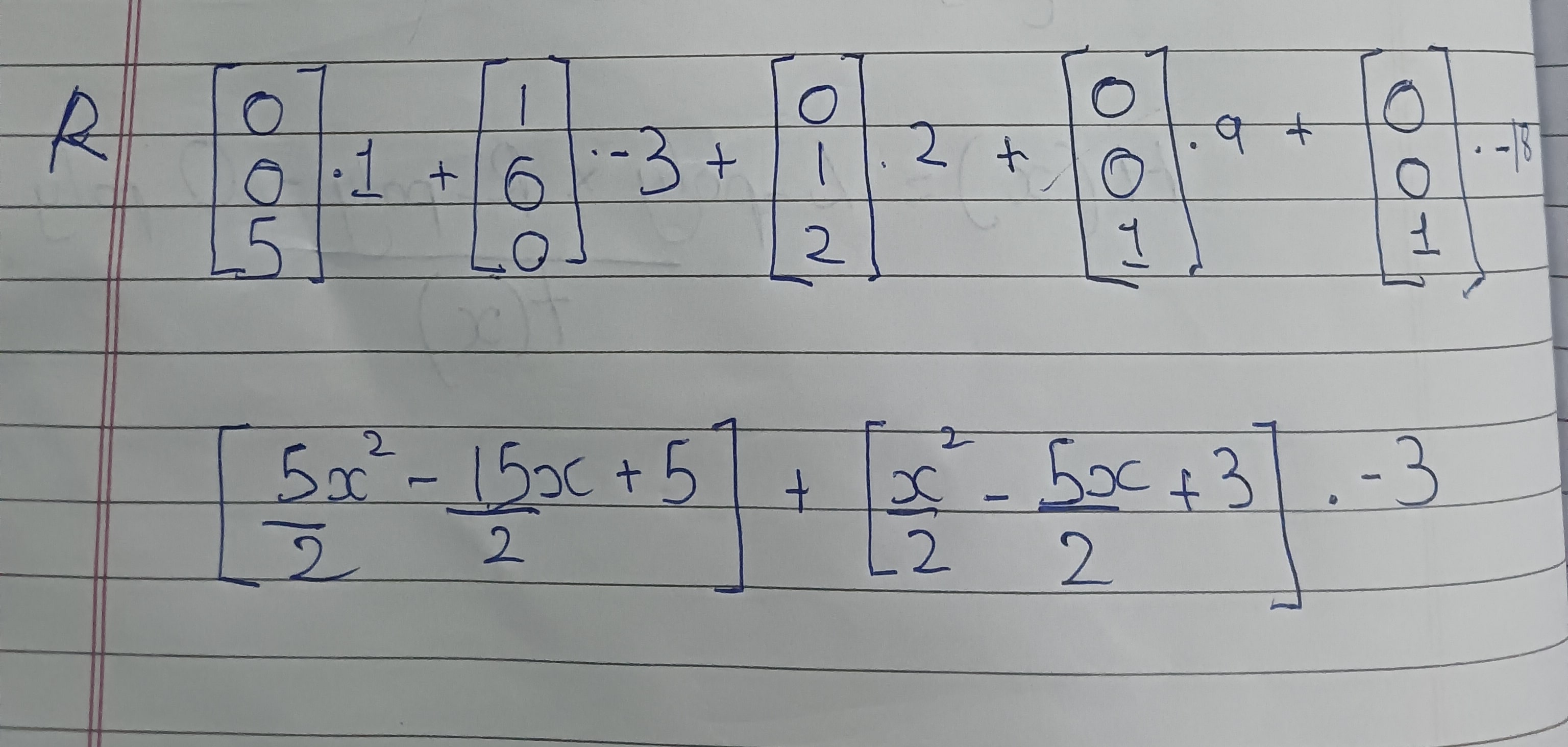
R matrix:
O matrix:
7. Getting the H(x) and T(x) polys.
T(x)
H(x)
8. Using the QAP formula we’re evaluating using a random value and verifying LHS = RHS.
